Bahas Soal Matematika   »   Limit   ›  

Hitunglah \( \displaystyle \lim_{x \to -\infty} \ x \ e^x \).

Pembahasan:

Jika kita substitusi \(x = -∞\) ke fungsi limitnya, kita peroleh bentuk tak tentu (∞)(0). Ini artinya kita perlu memodifikasi fungsi limitnya sehingga diperoleh bentuk tak tentu berupa pembagian 0/0 atau ∞/∞.

Kita bisa tuliskan limit dalam soal ini menjadi:

Sekarang jika kita substitusi \(x = -∞\) ke fungsi limit di atas, kita peroleh bentuk 0/0. Akan tetapi, kita harus hati-hati di sini. Jika kita gunakan Aturan L'Hospital, maka kita dapatkan hasil berikut:

Seperti yang bisa kita lihat dari hasil di atas, penggunaan Aturan L'Hospital tampak tidak berhasil. Kita bisa perbaiki ini dengan memodifikasi fungsi limitnya sehingga menjadi:

Dengan substitusi \(x = -∞\) ke fungsi limit yang baru ini, kita peroleh bentuk ∞/∞ sehingga jika diterapkan Aturan L'Hospital, maka kita peroleh hasil berikut:

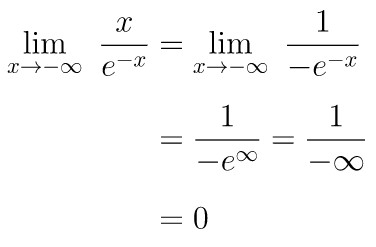
Jadi, hasil dari \( \displaystyle \lim_{x \to -\infty} \ x \ e^x = 0 \).